Futoshiki

Authors: Ruth Hoffmann and Gökberk Koçak

Problem

n x n board where each column and row is filled with the unique numbers from 1 to n, similar to a sudoku. In contrast to sudoku, there are less than and greater than symbols between cells indicating that one cell has to be filled with a number greater than (or less than) than the cell on the other side of the operator.

Essence Model

Let us look at the model first.

language Essence 1.3
given n : int
letting DOMAIN be domain int(1..n)
given hints : function (DOMAIN, DOMAIN) --> DOMAIN
given less_than : relation of ((DOMAIN, DOMAIN) * (DOMAIN, DOMAIN))
find board : matrix indexed by [DOMAIN, DOMAIN] of DOMAIN
such that
    forAll (hint,num) in hints .
        board[hint[1], hint[2]] = num,
    forAll i: DOMAIN .
        allDiff(board[i,..]),
    forAll j: DOMAIN .
        allDiff(board[..,j]),
    forAll (l,g) in less_than .
        board[l[1],l[2]] < board[g[1],g[2]]

The line by line explanation starts here.

given n : int

Defines the size of the matrix and the maximal number of elements that we will add.

letting DOMAIN be domain int(1..n)

We start at 1 and go up to n (for both the elements of the cells and the cell locations).

given hints : function (DOMAIN, DOMAIN) --> DOMAIN

Here we define which cells are already filled in using a function. We map the coordinates onto the number that is in that cell. It is important to notice that functions in essence are partial functions not total. This means that not everything gets mapped.

given less_than : relation of ((DOMAIN, DOMAIN) * (DOMAIN, DOMAIN))

Here we define where the relation symbols are placed, it depends on which way you read the symbol we are “only” modelling less than. So should there be a “greater than” signs between two cells, say (2,1) and (1,1) then we would order them as (1,1) is less than (2,1).

find board : matrix indexed by [DOMAIN, DOMAIN] of DOMAIN

We are now telling the solver that we are trying to find a n x n board with elements from 1 to n in each cell.

such that

This is the beginning of the constraints block.

forAll (hint,num) in hints .
   board[hint[1], hint[2]] = num,

This constraint defines the hints, so the cells that are filled in when we get the puzzle.

forAll i: DOMAIN .
    allDiff(board[i,..]),

This constraint defines that every cell in a row has to be a unique number between 1 and n.

forAll j: DOMAIN .
    allDiff(board[..,j]),

This constraint defines that every cell in a column has to be a unique number between 1 and n.

forAll (l,g) in less_than .
    board[l[1],l[2]] < board[g[1],g[2]]

Finally this constraint enforces the less than relation. l is the number that is the cell that contains the number that is less than then the cell g.

Instance

We save the instance in a .essence-param file.

letting n be 4
letting hints be function(
        (1,1) --> 2,
        (2,2) --> 2
)
letting less_than be relation(
        ((1,1) , (2,1)),
        ((4,2) , (3,2)),
        ((3,3) , (3,4)),
        ((3,4) , (4,4))
)

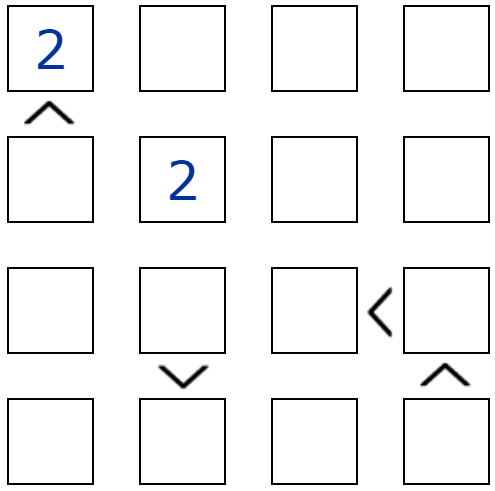
The .essence-param file contains the information about our starting board of a specific instance that we want to solve. See the picture at the beginning to see what it looks like.

letting n be 4

We are dealing with a 4 by 4 board.

letting hints be function(
        (1,1) --> 2,
        (2,2) --> 2
)

There will be two 2 s on the board given as a hint. One in the top left corner (1,1) and the second number 2 in cell (2,2).

letting less_than be relation(
        ((1,1) , (2,1)),
        ((4,2) , (3,2)),
        ((3,3) , (3,4)),
        ((3,4) , (4,4))
)

There are 4 relation symbols on the board, between cells.

Solving

Using the ESSENCE pipeline, we can solve our sample instance by typing the following:

conjure solve futoshiki-model.essence futoshiki-instance.essence-param

The result will be saved into a .solution file which will look something like this:

letting board be
        [[2, 1, 4, 3; int(1..4)], [4, 2, 3, 1; int(1..4)], [3, 4, 1, 2; int(1..4)], [1, 3, 2, 4; int(1..4)]; int(1..4)]
$ Visualisation for board
$ 2 1 4 3
$ 4 2 3 1
$ 3 4 1 2
$ 1 3 2 4